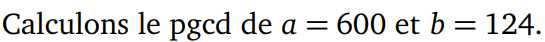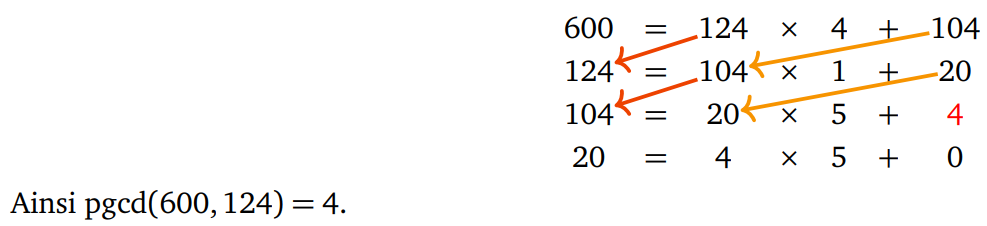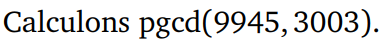L'algorithme d'Euclide est basé sur le lemme suivant :
Soit \(a,b\in\Bbb N^\star\)
Si on écrit la division euclidienne de \(a\) par \(b\), \(a=bq+r\) avec \(0\leqslant r\lt b\), alors $$\operatorname{pgcd}(a,b)={{\operatorname{pgcd}(b,r)}}$$
(Division euclidienne, Pgcd)
Démonstration :

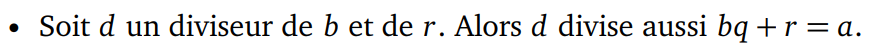
(Division - Diviseur - Divisibilité)
Algorithme d'Euclide :
Soit \(a\geqslant b\). On cherche \(\operatorname{pgcd}(a,b)\)
1. On effectue \(a=bq_1+r_1\) avec \(0\leqslant r_1\lt b\)
>- Si \(r_1=0\), alors \(\operatorname{pgcd}(a,b)=\operatorname{pgcd}(b,0)=b\)
>- Si \(r_1\gt 0\), on effectue \(b=r_1q_2+r_2\) et on applique le lemme